plane as the example. There
are six possible ways for the stability circle drawn on the plane as the
shown in Figure 17.
We take the input stability circle on plane as the example. There
are six possible ways for the stability circle drawn on the plane as the
shown in Figure 17.
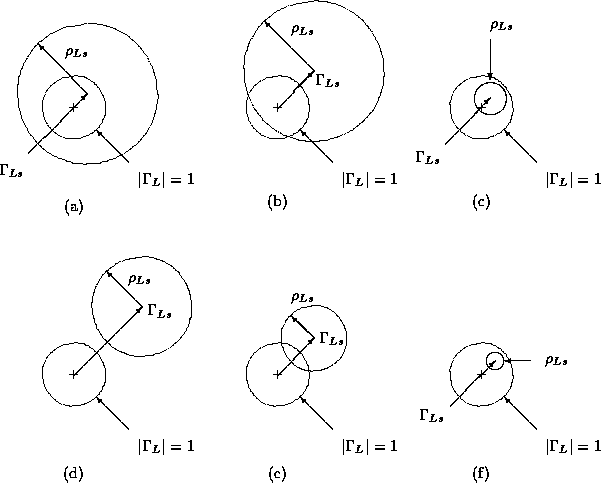
Figure 17: Six possible ways for the input stability circle
We consider only the case where 
and 
. The 
circle represents the
location where 
on the plane. Note that at the origin of the
plane, 
, hence a stable region. Therefore, the area including the origin of
the plane up to the circle is the stable region. We can find that
for all values of in Figure 17 (a) and 17 (d).
We re-examine the value of 
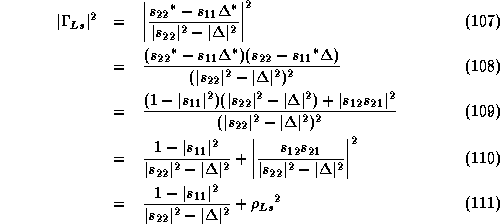
Case (i) 
this corresponds to Figure 17 (d), (e), (f). But Figure 17 (d) is unconditionally
stable, where
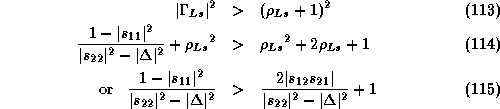
Because , we can re-write the condition as
Case (ii) 
this corresponds to Figure 17 (a), (b), (c). But Figure 17 (a) is unconditionally
stable, where
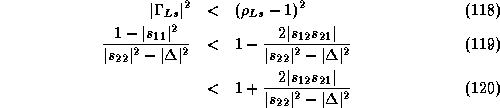
Because , we can re-write the condition as
Therefore, a necessary condition for unconditionally stability is
If we define
then K>1 is a necessary condition for unconditionally stability.
If we examine the Figure 17 (b), (c), (e), (f) again, we find that
Therefore, K > 1 is not the sufficient condition for stability. We must find a way to
distinguish Figure 17 (a) from Figure 17 (c). The difference between
two Figures is that 
in Figure 17 (a). Therefore
Combine with the inequality
Because for Figure 17 (a), (c). Finally, the necessary and sufficient conditions for unconditionally stability for the input port are
Therefore, the necessary and sufficient conditions for unconditionally stable two-port network are
and ,
and 
, and
Example In a 50 
system, a transistor has the following S-parameter at 1.3 GHz.
Examine the stability of the transistor.
Solution
The transistor is unconditionally stable.