Introduction to Quartz Frequency Standards - Crystal Unit Equivalent Circuit
![]() Forward to "Stability Versus Tunability".
Forward to "Stability Versus Tunability".
![]() Back to "Oscillator Basics".
Back to "Oscillator Basics".
![]() Back to the tutorial's table of contents.
Back to the tutorial's table of contents.
A quartz crystal unit is a quartz wafer to which electrodes have been applied, and which is hermetically sealed in a holder structure. (The wafer is often referred to as the "blank," or the "crystal plate".) Although the design and fabrication of crystal units comprise a complex subject, the oscillator designer can treat the crystal unit as a circuit component and just deal with the crystal unit's equivalent circuit.
The mechanically vibrating system and the circuit shown in Figure 2 are "equivalent," because each can be described by the same differential equation [6]. The mass, spring, and damping element (i.e., the dashpot) correspond to the inductor, capacitor and resistor. The driving force corresponds to the voltage, the displacement of the mass to the charge on the capacitor, and the velocity to the current.

Figure 2. Equivalent circuit of a mechanically vibrating system.
A crystal resonator is a mechanically vibrating system that is linked, via the piezoelectric effect, to the electrical world. Figure 3 shows a (simplified) equivalent circuit (of one mode of vibration) of a resonator, together with the circuit symbol for a crystal unit. A load capacitor CL is shown in series with the crystal. C0, called the "shunt" capacitance, is the capacitance due to the electrodes on the crystal plate plus the stray capacitances due to the crystal enclosure. The R1, L1, C1 portion of the circuit is the "motional arm," which arises from the mechanical vibrations of the crystal.
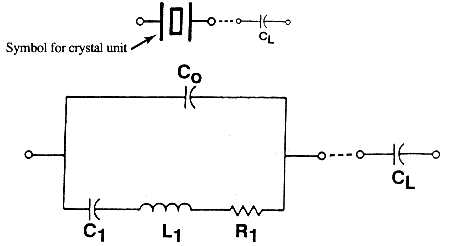
Figure 3. Equivalent circuit of crystal unit with load capacitor.
The C0 to C1 ratio is a measure of the interconversion between electrical and mechanical energy stored in the crystal, i.e., of the piezoelectric coupling factor, k. C0/C1 increases with the square of the overtone number; the relationship of C0/C1 to k and N is 2C0/C1 = [pN2/2k], where N is the overtone number. When a dc voltage is applied to the electrodes of a resonator, the capacitance ratio C0/C1 is also a measure of the ratio of electrical energy stored in the capacitor formed by the electrodes to the energy stored elastically in the crystal due to the lattice strains produced by the piezoelectric effect. Figure 4 shows the reactance versus frequency characteristic of the crystal unit. The C0/C1 is also inversely proportional to the antiresonanceresonance frequency separation (i.e., the polezero spacing) which is an especially important parameter in filter applications. The slope of the reactance vs. frequency curve near fS is inversely proportional to C1, i.e., DX/(Df/f) » 1/pfC1 near fS, where X is the reactance. C1 is, therefore, a measure of the crystal's "stiffness," i.e., its tunability.

Figure 4. Reactance versus frequency of a crystal unit.
When the load capacitor is connected in series with the crystal, the frequency of operation of the oscillator is increased by a Df' where Df' is given by
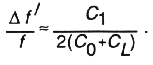
For the simple RLC circuit of Figure 2, the width of the resonance curve is inversely proportional to the quality factor Q, but in a crystal oscillator, the situation is complicated by the presence of C0 and by the fact that the operating Q is lower than the resonator Q. For a quartz resonator, Q = (2pfSC1R1)1. References 3, 5 and 6 contain further details on the equivalent circuit.
Some of the numerous advantages of a quartz crystal resonator over a tank circuit built from discrete R's, C's and L's are that the crystal is far stiffer and has a far higher Q than what could be built from normal discrete components. For example, a 5 MHz fundamental mode ATcut crystal may have C1 = 0.01 pF, L1 = 0.1 H, R1 = 5W, and Q = 106. A 0.01 pF capacitor is not available, since the leads attached to such a capacitor would alone probably contribute more than 0.01 pF. Similarly a 0.1 H inductor would be physically large, it would need to include a large number of turns, and would need to be superconducting in order to have a £5 W resistance.
![]() Forward to "Stability Versus Tunability".
Forward to "Stability Versus Tunability".
![]() Back to "Oscillator Basics".
Back to "Oscillator Basics".
![]() Back to the tutorial's table of contents.
Back to the tutorial's table of contents.